Sorting

Objective #1: Understand the basics of sorting.

• When you rearrange data and put it into a certain kind of order, you are sorting the data. You can sort data alphabetically, numerically, and in other ways. Often you need to sort data before you use searching algorithms to find a particular piece of data.
• There are a number of different sorting algorithms that are widely used by programmers. Each algorithm has its own advantages and disadvantages.
• View these animations of various sorting algorithms: sorting-algorithms.com
• The key field is the field upon which the data is sorted. For example, often last name is used as the key field when you sort a list of people's names. You would not use first name as a key field.
• A key value is a specific value that is stored within the key field. If you are sorting with the key field of last name then a key value at some point during the algorithm's execution would be "Minich".
• The input size is the number of elements in an array or ArrayList that are being sorted.
• There are two basic types of algorithms used to sort data: the incremental approach and the divide and conquer approach.
  • Using the incremental approach, one sorts the whole list at once usually using loops.
  • The divide and conquer approach splits the list up into parts and then sorts each part separately. This algorithm then puts the sorted parts together into a large sorted list.

Objective #2: Understand the selection sort.

• The selection sort is an incremental sorting algorithm.
  
• Every key value is examined starting at the beginning of the list. Assuming that you are sorting the list in ascending order, you use a temporary variable to "remember" the position of the largest key value. By the time you have examined every key value, you swap the key value that was the largest with the last key value in the list. Next, you repeat the process again from the beginning of the list, however, you will not need to compare anything to the new last key value in the list since you know it is the largest.
  
• This algorithm uses nested loops and is easy to code. However, it is quite inefficient since it continues processing even if the list is already sorted. Whether the original data is close to being sorted or not, this algorithm takes quite awhile since a lot of loop iterations and comparisons must be made.
  
• Characteristics
  • two nested loops
  • relatively efficient for small lists of less than 100 elements
  • many comparisons
  • only 1 exchange (swap) at the end of each pass
  • non-adjacent elements are compared
  • no boolean variable is used to allow for an early exit
  • a "temp variable" is used as a marker
    
    
• Here is an example of how the elements of an array (or ArrayList) would move after the passes of the outer loop in a selection sort. The underlined values are "set in concrete" as I like to say meaning that they are in their fixed locations.
  
  

  50 60 30 20 45
  20 60 30 50 45   the complete array is scanned from left to right & since 20 is the smallest it is swapped w/ the 50 in index position 0
  20 30 60 50 45   the array from index positions 1 thru 4 is scanned & since 30 is smallest it is swapped w/ the 60 in index position 1
  20 30 45 50 60   the array from index positions 2 thru 4 is scanned & since 45 is smallest it is swapped w/ the 60 in index position 2
  20 30 45 50 60   the array from index positions 3 thru 4 is scanned & since 50 is the smallest it is swapped w/ itself
  

• Here is an example of a selection sort
  
  

        
      public static void selectionSort(int[] arr)
      {
          for (int i = 0; i < arr.length - 1; i++)
          {
              int minIndex = i;
              int min = arr[minIndex];
   
  
              for ( int j = i + 1; j < arr.length; j++)
              {
         
                  if ( arr[j] < min)
                  {
                      minIndex = j;
                      min = arr[minIndex];
                  }
                 
             }
  
              int temp = a[minIndex];		// swap
              arr[minIndex] = arr[i];
              arr[i] = temp;
          }
          
      }
        
        

Objective #3: Understand the insertion sort.

• The insertion sort is another incremental sorting algorithm.
• Two lists are used throughout this algorithm. One list is sorted and the other is unsorted. The sorted list begins with one key value. Successively, one key value from the unsorted list is placed into the proper order with the smaller, sorted list. As more key values are placed into the sorted list, that list becomes larger.
• This is similar to the way a person usually organizes a hand of playing cards so Mr. Minich calls this the "poker-hand sort".
• The insertion sort is relatively quick for small lists that are close to already being sorted.
• Characteristics
  • two nested loops
  • boolean variable allows inner loop to exit early saving a bit of time here and there
  • compares non-adjacent elements
  • no exchanges (swaps), rather many elements must shift
  • a lot of comparisons are made slowing down this algorithm
  • very efficient when data is close to being in order
  • very inefficient when data is really out of order
    
    
• Here is an example of how the elements of an array (or ArrayList) would move after the passes of the outer loop in an insertion sort:
  
  50 30 60 40 45
  30 50 60 40 45    30 was compared to 50, the 50 is shifted to the right & the 30 is inserted to the left of the 50
  30 50 60 40 45    60 was compared to 50 & since it is greater than the 50 it stays where it is
  30 40 50 60 45    40 was compared to 60, the 50 & the 30 & since it is greater than 30 it is inserted between 30 & 50 while 50 & 60 are shifted right
  30 40 45 50 60    45 was compared to 60, the 50, & the 40 & since it is greater than 40 it is inserted between 40 & 50 while 50 & 60 are shifted right
  
  
• Here is an example of an insertion sort
  

  
      public static void insertionSort(int[] arr)
      {	
      	int j = 0;
          
          for (int i = 1; i < arr.length; i++)
          {
              int value = arr[i];       
              j = i;
  
              while (j > 0 && arr[j - 1] >= value)
              {
                  arr[j] = arr[j - 1];	// shift
                  j--;
              }
   
              arr[j] = value;		// insert
          }
          
      }
  
  

  
  

Objective #4: Understand the merge sort.

• The merge sort is a divide and conquer algorithm.
• The merge sort is a recursive algorithm.
• Mr. Minich invented this algorithm when he sorted his baseball cards when he was only 9 years old.
• The whole list is divided into lists that consist of one element a piece. Then, every two adjacent lists are merged into one larger sorted list. The process continues until one sorted list remains.
  
• Characteristics:
  • recursive, divide and conquer algorithm
  • takes lots of space (i.e. memory) since each of the log n stack frames contain a separate array variable.
    
• Here is an example of how the elements of an array (or ArrayList) would move after the passes of the outer loop in a mergesort:
  
  

  50 30 60 20 45 15 76 25
  50 30 60 20  |  45 15 76 25
  50 30  | 60 20  |  45 15  |  76 25
  50  | 30  | 60 |  20  |  45  | 15  | 76 |  25
  30 50  |  20 60  |  15 45 |  25 76
  20 30 50 60   |   15 25 45 76
  15 20 25 30 45 50 60 76
  

• Here is an example of a merge sort.
  

     public static void sort(int a[])
     {
          if (a.length > 1)
              mergeSort(a, 0, a.length);
     }
     
     public static void mergeSort(int a[], int start, int segLength)
     {
          // Divide the array in half and sort and merge the halves
          int half = segLength / 2;   
      
          // Sort each of the two parts of the arrays
          if (half > 1)
          {
              mergeSort (a, start, half);
          }
          
          if (segLength - half > 1)
          {
              mergeSort (a, start + half, segLength - half);
          }
      
          // Copy the two parts of the arrays & merge
          int t1[] = new int[half];
          int t2[] = new int[segLength - half];
          int i = start;
          
          for (int j = 0; j < half;)        
          {
              t1[j++] = a[i++];
          }
          
          for ( int j = 0; j < segLength - half;)   
          {
              t2[j++] = a[i++];
          }
          
          merge (a, start, t1, t2);    
     }
  
     public static void merge (int a[], int start, int t1[], int t2[]) 
     {
          int index = start;
          int end = start + t1.length + t2.length;
          int t1index = 0;
          int t2index = 0;
  
          while (t1index < t1.length && t2index < t2.length)
          {
              if (t1[t1index] <= t2[t2index])
                  a[index++] = t1[t1index++];
              else
                  a[index++] = t2[t2index++];
          }
          
          while (t1index < t1.length)
          {
              a[index++] = t1[t1index++];     
          }
          
          while (t2index < t2.length)
          {
              a[index++] = t2[t2index++];
          }
     }
      

  
  

The following information will not be tested on the AP exam or unit tests.

Objective #5: Understand the bubble & Shell sorts.

• The bubble and Shell sorting algorithms are not covered on the AP Computer Science exam.
• The bubble sort is an incremental sort which is usually faster than the insertion and selection sorts.
• A bubble sort works similarly to the release of CO₂ in carbonated soda.
• Beginning at one end of a list, adjacent key values are compared. Assuming that you are sorting the list into ascending order, these two key values would be swapped if the first was larger than the second. Next you compare the larger of the two to the next adjacent key value in the list, swapping if necessary. By the time that you compare the last two key values in the list, you know that the largest key value from the whole list will be in the last position. Using a loop, this process is continued (comparing adjacent key values) from the beginning of the list. However, you will not need to compare anything to the last key value in the list since you know it is the largest.
• A Boolean variable is used in a bubble sort to "remember" if any swaps are made on a particular sweep of the list. If a swap is made the variable might be set to TRUE. At the beginning of each successive sweep, the variable is set to FALSE. When a complete sweep of the loop has been made without any swaps, the variable will still be FALSE.
• The use of the Boolean variable causes this sort to only sweep the list one extra time after it has been fully sorted. This makes the bubble sort more efficient than a number of other incremental sorts.
• The Big Oh time performance of a bubble sort is O(n²) in the worst case. Because there is an early exit, it is also O(n) in the best case when the data is already in order.
• Characteristics:
  • two nested loops
  • adjacent elements are compared
  • many exchanges (i.e. swaps)
  • boolean variable allows outer loop to exit early possibly saving time
  • very inefficient when data is really out of order
  • very efficient when data is close to being in order due to the early exit

• The Shell sort is an incremental sort which was named after it's inventor, D. L. Shell. It is sometimes called the comb sort.
• This sorting algorithm is similar to the bubble sort but instead of comparing and swapping adjacent elements, elements that are a certain distance away from each other are compared and swapped. The certain distance can be called the gap size and might initially be set to half the input size.
• After each sweep, the gap is decreased until eventually adjacent elements are compared. A Boolean variable is used as it is in the bubble sort to add efficiency. It works the fastest when the successive gap sizes are relatively prime to each other.
• The Shell sort is much faster than other incremental sorts since very large and very small key values are quickly moved to the appropriate end of the list.
• The Big Oh time performance of a Shell sort is between O(n) and O(n²) but closer to O(n²) in the worst case. Because there is no early exit, it is also O(n(log n)²) in the best case.

Objective #6: Understand the quicksort.

• The quicksort algorithm is not covered on the AP Computer Science exam.
• The Quicksort is a divide and conquer algorithm and is more efficient than incremental sorts. It can be difficult to code though since it uses recursion or stacks.
• The original list is partitioned into two lists. One of the lists contains elements that are greater than the first original element. The second list contains elements that are less than or equal to the first original element. Then, each of these two partitions are partitioned using the same algorithm. Eventually, partitions will have only one element each. When this happens, that single-item partition is considered to be sorted and only partitions with multiple-items are partitioned. When every partition consists of only a one element, the partitions are placed into order to make a fully sorted list.
• The Quicksort is horribly slow when the original data is mostly in order. The partitions are imbalanced in this case. It is paradoxically beneficial to shuffle the data first before applying the quicksort especially if you think the data may be partially sorted.
• The Big Oh time performance of a Quicksort is between O(n log n) in the best case and O(n²) in the worst case.
• Characteristics:
  • recursive, divide and conquer algorithm
  • on average, this is the fastest sorting algorith

Objective #7: Apply Big-O notation to sorting & searching algorithms.

• Big-O notation is not covered on the AP Computer Science exam.
• Big-O notation is a method of classifying algorithms with regard to the time and space that they require. The O refers to "on the order of".
• Formal definition of big-O: Suppose there exists some function f(n) for all n > 0 such that the number of operations required by an algorithm for an input of size n is less than or equal to some constant C multiplied by f(n) for all but finitely many n. The algorithm is considered to be an O[f(n)] algorithm relative to the number of operations it requires to execute.
• This algorithm is classified as O[f(n)].
• There is some point of intersection between the graph of the algorithm and the function f(n) where the function "bounds" the algorithm. That is, the function will lie above the algorithm for any given point n.
• If n is really small, it does not really matter what algorithm is used to sort or search since the time difference will be negligible.
  
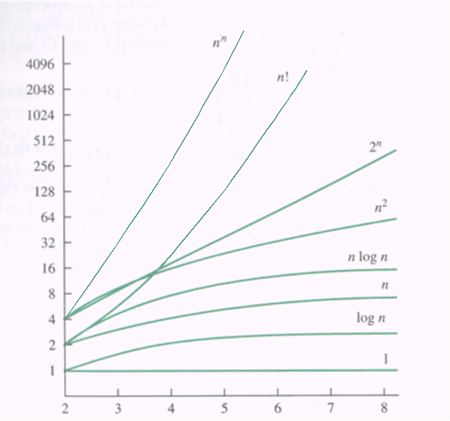
• Common big-O categories:
  
  

  O(1)	constant	push & pop stack operations; insert & remove queue operations
  O(log n)	logarithmic	binary search; insert & find for binary search tree; insert & remove for a heap
  O(n)	linear	traversal of a list or a tree; sequential search; finding max or min element of a list
  O(n log n)	"n log n"	quicksort, mergesort
  O(n2)	quadratic	selection sort; insertion sort; bubble sort
  O(n3)	cubic
  O(an)	exponential	recursive Fibonacci; Towers of Hanoi

The linear, quadratic, and cubic algorithms are also called polynomial algorithms.

• Since it is true for any a, b > 0 and a, b <> 1:
  
  log₂ n = log₁₀ n / log₁₀ 2
  
  then
  
  log₁₀ n = C log₂ n
  
  where C is a constant. Therefore, O(log₂ n) is really the same as O(log n).
  
• O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(n³) < O(aⁿ)
• Divide and conquer algorithms like the quicksort, mergesort, & the binary search are very efficient since they have logarithmic growth.
• If an algorithm is O(n²) then it is also O(n^a) where a > 2 since the n^a bounds n².
• To determine an algorithms big-O category, it is most useful to analyze its loops.
• In analyzing the loops of an algorithm, you must come up with some function f(n) where C * f(n) parallels (or "bounds") the actual number of operations within the algorithm as closely as possible. The constant C is known as the constant of proportionality and ultimately makes no difference when comparing two functions with the same order of magnitude. The order of magnitude is the degree of the function (the largest exponent of n) or a logarithmic or exponent term.
• In any derived function f(n), one term will be the dominant term. A dominating function then is a function f(n) with the dominant term of the original derived function. For example, if you come up with the function f(n) = n² + n log ₂ n + 5, the dominating function is n² since n² is the dominant term in f(n).
  Examples: n dominates log n, n log n dominates n, n³ dominates n² and a² dominates n^m
• When an outer loop iterates from 1 to n-1 and a nested loop iterates from 0 to i-1 (where i is the loop variable in the outer loop), the inner loop will iterate a total of 1 + 2 + 3 + .... + (n - 1) times. This is equal to n(n - 1)/2 which is the number of terms multiplied by the average of the first and last terms. Since n² ends up being the dominant term in the polynomial, this explains the O(n²) category of several of the algorithms we will be analyzing.
• See this big-O sorting algorithm summary & Big-Oh Time Efficiency Examples
• Wikipedia entry "Sorting Algorithm" that includes Big-Oh classification for many sorts
• Big-Oh chart from the Litvin's
• Another Big Oh chart
• Here is a graph of the common big-O categories courtesy of http://www.cs.odu.edu/~toida/nerzic/content/function/growth.html. Note that in order to "fit" all of the functions on the graph, the vertical time axis is marked in a way that each marking is double the previous marking.