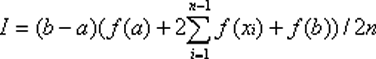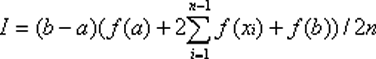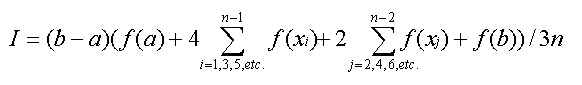COMPUTING INTEGRALS

Objective #1: Explain and use the Trapezoidal Rule for numerical integration.

• The Trapezoidal Rule for finding the area under a curve (often considered a method of integration) involves using straight line segments to form a trapezoidal region. The area of the region is then calculated using the formula for finding the area of a trapezoid. This rule can be expressed as
  
  I = (b - a) * ( f(a) + f(b) ) / 2
  
  where a and b are the endpoints of the region and f is the function.
  
  
• You can improve the accuracy of this method by dividing the integration interval into more trapezoidal regions by drawing more line segments. Then, the sum of all of the regions is computed and used as an approximation for the total area under the curve (i.e. the integral of the function.) This technique is one form of multiple-application integration.
  
  The Multiple-Application Trapezoidal Rule is
  
  
  
  
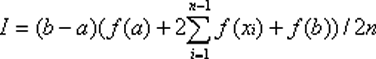
• For some "nice" functions, this method is fine for obtaining an accurate integral. But, sometimes so much computational work must be done that other methods are more efficient.
  
  
• Round-off error can limit the ability for this method to determine an integral.
  

Objective #2: Explain and use Simpson's 1/3 Rule and Simpson's 3/8 Rule for numerical integration.

• Simpson's 1/3 Rule calls for using parabolas to approximate a function's curve. Usually by picking triplets of equally-spaced values for x and forming a parabola from each set of 3 points, a better approximation of the area under a curve can be made than using the Trapezoidal Rule.
  
  
• In general, Simpson's Rule can be used to compute an integral more efficiently and/or more accurately than the Trapezoidal Rule since it is a higher-order polynomial and will probably provide a "better fit" for the function.
  
  
• The following formula for Simpson's 1/3 Rule can be used where there are 2 segments and 3 points across the region to be integrated:
  
  I = (b - a) * (f(x0) + 4 * f(x1) + f(x2)) / 6
  
  where x0 is the left endpoint of the interval, x2 is the right interval and x1 is the midpoint of the interval. The textbook presents this formula as Equation 13.13 on p. 702.
  
  
• The multiple application version of Simpson's 1/3 Rule can be used to obtain a more accurate approximation of an integral as long as the number of segments that the interval is divided into (the variable n in the formula below) is even.
  
  
• The Multiple-Application Simpson's 1/3 Rule is
  
  
  
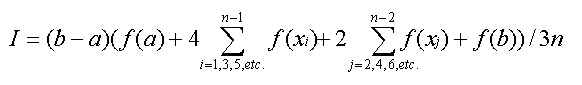
• Simpson's 1/3 Rule is limited to situations where one has divided the original interval into an even number of segments with an odd number of points. However, Simpson's 3/8 Rule can be used if one has an odd number of segments formed from an even number of points.
  
  
• The following formula for Simpson's 3/8 Rule can be used where there are 3 segments and 4 points:
  
  I = (b - a) * (f(x0) + 3 * f(x1) + 3 * f(x2) + f(x3)) / 8
  
  where x0 is the left endpoint of the interval, x3 is the right endpoint, and x1 and x2 are equally spaced points within the interval.