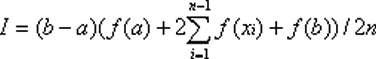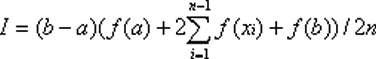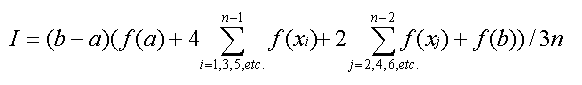FINDING ROOTS

Objective #1: Explain the concept of roots to an equation and determine the number of roots to an equation.

• A root of an equation is a value for x that makes a given function f(x) equal to 0.0.
• Two curves, f(x) and g(x), intersect where f(x) - g(x) = 0.0, so a root to F(x) = f(x) - g(x) is a point of intersection between the two functions.
• A polynomial of degree n (where n is the highest power of the independent variable x) has at most n roots that can include complex numbers (with i = square root of -1) and multiple roots.
• Transcendental functions which involve trig, log, and/or exponential functions can have rational or irrational roots. However, since the computer's number system is finite (due to the finite range of data type's, maximum precision with each data type, and processor's computational methods), we usually use the same algorithms for finding roots to transcendental functions as well as polynomials.
• Transcendental functions can also have an infinite number of roots. Of course, a computer cannot find or display an infinite number of roots so you have the responsibility in such cases to terminate your program or simplify a root-finding algorithm.
• See p. 672 for examples of the types of functions that are typically encountered in root solving.
  
  
• The quadratic formula is only useful for general quadratic equations which of course have a degree of 2. Use the quadratic formula
  
  r = (-b +/- sqr(pow(b, 2) - 4 * a * c)) / 2 * a
  
  to solve for r, the roots of a general quadratic equation of the form a * POW(x, 2) + b * x + c = 0

Objective #2: Use graphical methods to find or predict roots.

• Our root-solving techniques will first require that you either specify an initial interval that is known to contain a root or that you provide an initial guess for the root.
• It is wise to initially draw a graph for a function when you wish to find its roots to determine an initial guess for a root.
• It may take a significant amount of time to obtain a decent initial guess for an equation's root.
• In fact, which of the following methods (Bisection, False Position, etc.) that you choose must be done wisely and with great care. Otherwise, your algorithm may be slow or even useless in particular cases.

Objective #3: Explain and use the Bisection Method to finding roots.

• The Bisection Method is a systematic, iterative method for finding a root to a continuous function if you know that at least one root exists between two given points in the domain. It is easier to use and more dependable if you know for sure that exactly one root exists within a given interval.
  
  
• The algorithm picks midpoints x within the interval (a, b) and after computing the f(x), you change one of the interval endpoints depending on whether the f(x) is greater or less than the f(a) or f(b). Then, half of the original interval is discarded and the midpoint is assigned to one of the endpoints. After a few iterations, the algorithm yields an approximation of the root given a specified tolerance.
  
  
• The only inputs necessary for the Bisection Method would be the function itself, the tolerance, and the endpoints of the original interval. You may also wish to have the user specify a maximum number of iterations.
  
• The success of the Bisection Method is based on the size of the interval. That is, the larger the interval that contains the root, the more iterations and the longer time it will take to find a suitable approximate root.
  
  
• The number of iterations it would take to predict an approximated root with a specified tolerance can be predicted when using the Bisection Method. If you are required to find a root to within a tolerance, d, then the number of iterations, n, can be determined as
  
  (b - a) / pow(2, n) < d
  
  where a and b are the original endpoints and n is the number of iterations. (See p. 676)
  
  You can also use the equation
  
  ( log₂ ((b - a)/ d )) < n
  
  or
  
  (log ((b - a)/d))/log 2 < n (since log₂ x = log x / log 2)
  
  to determine the smallest whole number n that represents the number of iterations that will guarantee an acceptable approximated root.
  
  
• Study and understand Program 14.1 on p. 762. You will be expected to explain this program's algorithm in essay form. You will also be expected to be familiar enough with this program to fill in missing sections (variables, expressions, and even whole statements).
  
  
• Notice that f(x1), f(x2), and f(x3), are not all computed on each and every iteration of the for loop. This would lead to extra unnecessary computations, slowing the down the processor and increasing the overall program execution time.
  
  
• Also, notice that a number of diagnostic messages are included exposing potential problems such as excessive iterations and no noticeable roots within the specified interval.
  
  
• See the the Interactive Root Finder for any interesting view and tutorial of finding roots with the Bisection Method.

Objective #4: Explain and use the False Position Method (aka Regula Falsi Method) for finding roots.

• The Bisection Method as explained in Ch. 14, Section 2 is not the most sophisticated algorithm for finding real roots in such conditions. It can be considered to be a use of brute force. It can be slightly improved by interpolating the successive approximated roots between the function's values at the interval endpoints. Modifying it in this way leads to what is called the False Position Method. The False Position Method almost always converges more quickly than the Bisection Method.
  
  
• Basically, the statement
  
  x2 = (x1 + x3) / 2;
  
  in the Bisection Method algorithm is replaced by the statement
  
  x2 = x1 - (x3 - x1) * f1 / (f3 - f1);
  
  to turn it into the False Position Method. The Bronson textbook uses slightly different code in Program 14.2 due to its particular form of the algorithm. Note that the text uses the convergence criterion of fractional size of the search interval (current interval / original interval) on p. 685.
  
  
• The False Position Method also guarantees that you will find a root within a specified tolerance if the function is continuous and there is at least one root in the original interval.
  
  
• Study and understand Program 14.2 on p. 770. You will be expected to explain this program's algorithm in essay form. You will also be expected to be familiar enough with this program to fill in missing sections (variables, expressions, and even whole statements).
  
  
• Since the values of f1 and f3 could be very close, their difference could be so close to zero to cause round-off errors (even when using a double data type). This is a potential problem that could lead to poor results depending on the nature of the function.
  
  
• The only inputs necessary for the Method of False Position would be the function itself, the tolerance, and the endpoints of the original interval. You may also wish to have the user specify a maximum number of iterations.
  
  
• By introducing and using a relaxation factor to draw the interpolating segments, the method converges more quickly. Our textbook calls this method the "Modified Regula Falsi Method." This artificially reduces the slope of the interpolating line to find the next predicted root value. Eventually, after enough approximations, the predicted roots alternate between the left and right sides of the interval. This modified version of False Position is more efficient than the one without the relaxation factor and the Bisection Method.
  
  
• The textbook suggests using a relaxation factor of 0.9 unless you can perform the sophisticated analysis to determine a better relaxation factor for the given function.
  
  
• It is NOT possible to predict the number of iterations necessary to find a suitable root with either form of the False Position Method. Therefore, the programmer should include a check for an excessive number of iterations. The success of the False Position Method is based on the size of the function not the size of the interval. That is, the larger the function (i.e. f(b) - f(a)) the quicker the method will hone in on a suitable approximate root. However, the success of the Modified False Position Method is based on the size of the interval.
  

COMPUTING INTEGRALS

Objective #5: Explain and use the Trapezoidal Rule for numerical integration.

• The Trapezoidal Rule for finding the area under a curve (often considered a method of integration) involves using straight line segments to form a trapezoidal region. The area of the region is then calculated using the formula for finding the area of a trapezoid. This rule can be expressed as
  
  I = (b - a) * ( f(a) + f(b) ) / 2
  
  where a and b are the endpoints of the region and f is the function.
  
  
• You can improve the accuracy of this method by dividing the integration interval into more trapezoidal regions by drawing more line segments. Then, the sum of all of the regions is computed and used as an approximation for the total area under the curve (i.e. the integral of the function.) This technique is one form of multiple-application integration.
  
  The Multiple-Application Trapezoidal Rule is
  
  
  
  
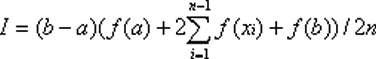
• Equation ?? on p. ?? is the Trapezoidal Rule.
  
  
• For some "nice" functions, this method is fine for obtaining an accurate integral. But, sometimes so much computational work must be done that other methods are more efficient.
  
  
• Round-off error can limit the ability for this method to determine an integral.
  
  
• In general, Simpson's Rule can be used to compute an integral more efficiently and/or more accurately since it is a higher-order polynomial and will probably provide a "better fit" for the function.
  
  
• Analyze the function trapezoid in integration demo program #1.
  
  
• See pp. 584 - 595 in the textbook, Numerical Methods for Engineers, for more information on the Trapezoidal Rule. A copy of this textbook can be found in the library.

Objective #6: Explain and use Simpson's 1/3 Rule and Simpson's 3/8 Rule for numerical integration.

• Simpson's 1/3 Rule calls for using parabolas to approximate a function's curve. Usually by picking triplets of equally-spaced values for x and forming a parabola from each set of 3 points, a better approximation of the area under a curve can be made than using the Trapezoidal Rule.
  
  
• The following formula for Simpson's 1/3 Rule can be used where there are 2 segments and 3 points across the region to be integrated:
  
  I = (b - a) * (f(x0) + 4 * f(x1) + f(x2)) / 6
  
  where x0 is the left endpoint of the interval, x2 is the right interval and x1 is the midpoint of the interval. The Bronson textbook presents this formula as Equation 13.13 on p. 702.
  
• The multiple application version of Simpson's 1/3 Rule can be used to obtain a more accurate approximation of an integral as long as the number of segments that the interval is divided into (the variable n in the formula below) is even.
  
• The Multiple-Application Simpson's 1/3 Rule is
  
  
  
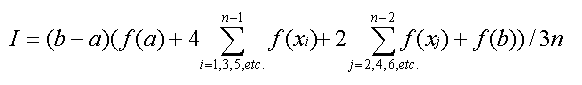
• Simpson's 1/3 Rule is limited to situations where one has divided the original interval into an even number of segments with an odd number of points. However, Simpson's 3/8 Rule can be used if one has an odd number of segments formed from an even number of points.
  
  
• The following formula for Simpson's 3/8 Rule can be used where there are 3 segments and 4 points:
  
  I = (b - a) * (f(x0) + 3 * f(x1) + 3 * f(x2) + f(x3)) / 8
  
  where x0 is the left endpoint of the interval, x3 is the right endpoint, and x1 and x2 are equally spaced points within the interval.
  
  
• Analyze the functions simpson1_3 and simpson3_8 in integration demo program #1.
  
  
• See pp. 595-607 in the textbook, Numerical Methods for Engineers, which can be found in the library.
• See pp. 617 - 622 in the supplemental textbook, C Program Design for Engineers, for more information on Simpson's Rule. A copy of this textbook can be found in the library.

SOLVING SYSTEMS OF LINEAR EQUATIONS

Objective #7: Explain and use 3 methods for solving simultaneous linear equations by hand.

• There are at least 3 general methods for solving sets of simultaneous linear equations by hand. However, these techniques are often only practical when the number of equations is three or less. A computer should be used when there are more equations.
  
  
• Three methods for solving sets of simultaneous equations:
  
  
  • The Graphical Method - Since linear equations form straight lines, it is not difficult to graph them on the Cartesian plane. If you are solving a set of 2 linear equations and they intersect, the solution of is the point of intersection. If there are three equations and the planes that they represent intersect in a three-dimensional coordinate system, the point of intersection is the solution. In either case, if they do not intersect, then there are no solutions and it is said that the system is singular. If the intersection is a line or a plane, then there are infinite solutions and it is said to be a singular system as well. However, if the point of intersection is difficult to determine because two lines or planes are very close to being singular, then the system is said to be ill-conditioned. Note that ill-conditioned systems pose problems for numerical solutions and computer algorithms due to round-off errors.
    
    
  • Cramer's Rule - The determinant of a 2 x 2 matrix of the form
    
    a11 a12
    a21 a22
    
    is D = a11*a22 - a21 * a12
    
    The determinant of a 3 x 3 matrix of the form
    
    a11 a12 a13
    a21 a22 a23
    a31 a32 a33
    
    is D = a11 * (a22 * a33 - a32 * a23) - a12 * (a21 * a33 - a31 * a23) + a13 * (a21 * a32 - a31 * a22)
    
    Cramer's Rule shows that each unknown in a system of linear equations is the fraction formed by the fraction where the numerator is the determinant of the 3x3 matrix formed by substituting the column of coefficients of the unknown by the constants (e.g. the constant b1 where a11x1 + ... + a13x3 = b1 is the first equation) and the denominator is the determinant of the matrix formed by the equations' coefficients.
    
    
  • Another technique for finding the determinant of a 3 x 3 matrix is called the Sarrus Rule. See this link for more details.
    
    
  • Elimination of Unknowns - Multiply one equation by a constant so that it is possible to combine the two equations and eliminate one of the unknowns. The remaining unknown can then be easily solved and substituted back into either original equation to determine the other unknown.
    

Objective #8: Explain and use a computer algorithm for using Gauss Elimination.

• Gauss elimination (sometimes called Gaussian elimination) is a scheme which uses the Elimination of Unknowns process as described above to solve a set of equations, however large.
  
  
• Two phases:
  
  
  • forward elimination
    • The goal during this phase is to reduce the set of equations to an upper triangular system where the only nonzero entries in the matrix form a triangle in the upper-right corner of the matrix that is augmented to the right with a vector formed by the equations' constants. This matrix is called an augmented matrix.
    • A pivot equation is chosen which has the maximum coefficient value in the first column. The maximum coefficient value in this column is called the pivot coefficient (or pivot element). If necessary, you can swap any two rows (i.e. equations) in the augmented matrix in order to place the pivot equation at the top of the matrix.
    • The pivot equation is divided by the value equal to its pivot coefficient as long as this does not cause division by zero. This process is called normalization.
    • The coefficient of the term in the same column on the next equation is multiplied with the pivot equation so as to be able to eliminate that term when the two equations are added or subtracted.
    • This process is continued until all of this term's coefficients in the other equations are eliminated.
    • These three operations can be and are performed on the augmented matrix formed by the system of equations:
      
      
      1. You can multiply any row of the augmented matrix by a nonzero number.
      2. You can add any row of the augmented matrix to any multiple of another row.
      3. You can swap any two rows.
         
         
    • The following pseudocode to perform forward elimination could be used:
      
      For k = 1 to n-1
         For i = k+1 to n
            factor = Aik / Akk
            For j = k+1 to n
               Aij = Aij - factor * Akj
            Bi = BI - factor * Bk
      
      
  • back substitution
    • After an upper-triangular matrix has been formed, the last equation will indicate the solution for one of the unknowns.
    • This result can be back-substituted in the next-to-last equation in order to evaluate one of the other unknowns.
    • This process can be continued until all of the unknowns have been determined.
    • The following pseudocode to perform back substitution could be used:
      
      Xn = Bn / Ann
      For i = n-1 to 1 by -1
         sum = 0
         For j = i+1 to n
            sum = sum + Aij * Xj
         Xi = (BI - sum) / Aii
      
      
• Potential errors
  • Division by zero - The method of Gauss Elimination outlined above is sometimes called Naive Gauss Elimination because it is possible to divide by zero during the forward elimination or the back substitution phases when blindly following the algorithm. The process called partial pivoting is used to swap two rows of coefficients when necessary in order to place the maximum coefficient of a given term in the proper row and avoid division by zero. (Complete pivoting involves swapping columns but is rarely used due to extra, difficult-to-program side requirements.)
    
    The following pseudocode for partial pivoting could be used:
    
    p = k
    big = abs(Akk)
    For ii = k+1 to n
       dummy = abs(Aii,k)
       If dummy > big
          big = dummy
          p = ii
    If p != k
       For jj = k to n
          dummy = Ap,jj
          AP,jj = Ak,jj
          AK,jj = dummy
       dummy = Bp
       BP = Bk
       Bk = dummy
    
    
  • Round-off errors - As always, a computer must round off values in order to compute and store values. In systems, with large numbers of equations, these round-off errors can snowball (propagate) into larger errors as the algorithm proceeds. Also, if some coefficients are extremely large and others are very small, round-off errors tend to affect answers. So scaling the equations so that the maximum coefficient for each term is the value one will decrease round-off error. Sometimes, scaling is just used to determine if equations should be pivoted. Always, back-substitute results into the original equations of the system in order to check your answers to decide if round-off error is significant.
  • Ill-conditioned systems - If a small change in one or more coefficients' values leads to a great change to the solution of the system, the system is said to be ill-conditioned. Otherwise, the system is considered to be well-conditioned. In fact, round-off errors can cause large errors in the computed solutions in ill-conditioned systems. It is sometimes possible to scale the equations so that the maximum element in any row is 1. Using the most precise data type is advisable to avoid having an ill-conditioned system spoil your attempt at finding a solution.
  • Singular systems - If a system is singular, then it's determinant is zero. Furthermore, the determinant of a triangular system can easily be computed by multiplying the diagonal entries. Therefore, it is worthwhile to check the determinant of a system with this simple computation after forward elimination.
    
    
• Pseudocode for Gauss Elimination - Notice that the scaling is not used to manipulate the equations only to check if pivoting should be performed. Also, notice that the determinant is checked by computing the diagonal terms to find singular systems. The term er is used to indicate whether or not a singular system has been found. The term tol is set by the user to determine the user's tolerance for near-zero occurrences.
  
  Sub Gauss(A,B,n,X,tol,ER)
     Dim S(n)
     ER= 0
     For i = 1 to n
        Si = abs(Aij)
        For j = 2 to n
           If abs(Aij) > Si Then Si = abs(Aij)
     Call Eliminate(A, S, n, B, tol, ER)
     If ER != -1 Then Call Substitute(A, n, B, X)
  
  Sub Eliminate(A,S,n, B, Tol, ER)
     For k = 1 to n-1
        Call Pivot(A, B, S, n, k)
        If (abs(Akk/Sk) < tol Then
           ER = -1
           break
        For i = k+1 to n
           factor = Aij
           For j = k+1 to n
              Aij = Aij - factor * Bk
     If abs(Akk/SK) < tol Then ER = -1
  
  Sub Pivot(A, B, S, n, k)
     p = k
     big = abs(Akk / SK)
     For ii = k+1 to n
        dummy = abs(Aii,k / Sii)
        If dummy > big Then
           big = dummy
           p = ii
     If p != k Then
        For jj = k to n
           dummy = AP,jj
           AP,jj = AK,jj
           AK,jj = dummy
        dummy = BP
        BP = Bk
        Bk = dummy
  dummy = Sp
  SP = SK
  SK = dummy
  
  Sub Substitute(A, n, B, X)
     Xn = Bn/Ann
     For i = n-1 to 1 by -1
        sum = 0
        For j = i+1 to n
           sum = sum + Aij * Xj
        XI = (BI - sum)/Aii
  
  
• Another form of Gauss Elimination pseudocode is found on p. 434 in C Program Design for Engineers:
  
  p = 0
  For i = p to n-1
     pivot using the maximum pivot strategy
     if a solution is still possible
        scale the pivot row
        eliminate the coefficients beneath the pivot row
    go to the next row
  If last coefficient is 0
     no unique solution exists
  Else if there is a solution
     scale the last row
  

Objective #9: Explain and use a computer algorithm for using Gauss-Jordan's Method.

• The Gauss-Jordan Method is a more extensive variation of Gauss Elimination.
• When an unknown is eliminated, it is eliminated from all other equations rather than just the ones below the current pivoting equation. In this manner, the final matrix contains nonzero values on the diagonal rather than a triangular matrix. Only the diagonal elements are nonzero. The rows are also normalized by dividing each one by its pivot element. The result is that the identity matrix is formed where all diagonal coefficients are the value 1.
• Back-substitution is not necessary when using the Gauss-Jordan method since the result is the identity matrix.
• The Gauss-Jordan method requires more work and more operations (such as division, multiplication, etc.) than Gauss elimination therefore plain Gauss elimination is preferred.